[Données synthétiques] - Dis papa, comment on fait les données ? 1/2
Rédigé par Alexis Léautier
-
18 octobre 2022L'appétit en données de tous les secteurs grandissant, de nouvelles techniques émergent pour alimenter encore et toujours les serveurs en données de toutes sortes. La synthèse de données, en produisant des données à partir de données pourrait répondre aux besoins des réutilisateurs dans le respect des obligations de confidentialité. Mais les données synthétiques sont-elles vraiment anonymes ?
Sommaire :
[Données synthétiques] - Dis papa, comment on fait les données ? 1/2
[Données synthétiques] - Et l’Homme créa les données à son image 2/2
L’effervescence récemment observée dans le milieu académique concernant la synthèse de données vient en réponse à un problème posé en 1993 et pourtant toujours d’actualité. Alors qu’il cherchait à rendre publiques les données du recensement de la population collectées par le US Census Bureau, particulièrement utiles à l’élaboration de statistiques, Donald Rubin, professeur en statistiques à Harvard, fut confronté au problème de la confidentialité des données. En effet, les données concernées permettant d’identifier les individus, leur publication en l’état ne semblait pas possible. Il proposa alors une solution issue du domaine des statistiques : publier des données générées par des méthodes mathématiques, représentatives des données réelles mais permettant de s’affranchir de l’obligation de confidentialité attachée aux données sources.
Cette première donna lieu au développement de techniques plus élaborées de synthèse de données tabulaires ou en séries, jusqu’à l’introduction de méthodes d’apprentissage profond permettant également de générer images et vidéos. En particulier, une approche nouvelle, appelée antagoniste, introduite par (Goodfellow et al., 2014), permit d’améliorer sensiblement les résultats obtenus. Toutefois, si la majorité de ces techniques de génération sont aujourd’hui bien maîtrisées, le marché des données synthétiques est aujourd’hui en pleine croissance[1] en raison du besoin exponentiel en données exprimé par certaines industries. Parmi ces dernières figurent l’industrie automobile et en particulier les constructeurs de voitures autonomes tels que Waymo qui réalise la majorité de ses tests en environnement simulé. Toutefois, de nombreuses autres industries ont les yeux rivés sur cette technique, car elle pourrait permettre de rendre accessible une très grande variété de données dont toute exploitation était jusqu’alors restreinte par divers types de contraintes : confidentialité, propriété intellectuelle, difficultés pratiques liées à la collecte, coût de collecte ou d’acquisition, etc.
Genèse de la synthèse
Synthétiser sans modération
Les données synthétiques peuvent être utilisées dans de nombreux contextes et de multiples manières. En premier lieu, on distingue trois types d’ensembles de données où la synthèse aura été utilisée : les données entièrement synthétiques, partiellement synthétiques ou hybrides.
- Un ensemble est entièrement synthétique lorsque les données qu’il contient ont été entièrement générées par un modèle. En pratique, les caractéristiques de l’ensemble de données réelles (comme sa distribution statistique) sont extraites, puis l’ensemble de synthèse est généré afin de reproduire ces caractéristiques tout en introduisant de l’aléatoire.
- Seules certaines des variables d’un ensemble de données partiellement synthétique auront été générées selon le procédé précédent. On pourra appliquer ce protocole à un ensemble contenant par exemple des données particulièrement identifiantes comme l’âge, ou l’adresse.
- Un ensemble de données hybrides aura été généré à partir de l’ensemble réel et d’un ensemble entièrement synthétique afin de mieux représenter les spécificités de l’ensemble réel. Pour cela, on pourra par exemple, pour chacun des points réels, sélectionner le point le plus proche dans l’ensemble synthétique : cela permettra de reproduire certains cas particuliers de l’ensemble source sans utiliser directement les données réelles.
Les modalités d’utilisation des données synthétiques varient également. Certains cas d’usage ne nécessitent qu’un unique ensemble de données synthétiques, c’est le cas par exemple lorsque les données ne sont pas accessibles, ou trop confidentielles pour être partagées directement (pour des données de santé, de recensement de la population, etc.). Dans d’autres situations, l’accès au dispositif de génération de données au moins partiel sera nécessaire afin de produire un nombre important d’ensembles de données en faisant varier certains paramètres ou de manière aléatoire, permettant ainsi de représenter une situation avec un objectif d’exhaustivité ou pour simuler des situations spécifiques rares en pratique (pour des simulations de navigation de voitures autonomes, de détection de fraudes bancaires, etc.).
D’accord, mais pourquoi ?
Ces différentes modalités d’utilisation répondent en pratique à des besoins différents. Ceux-ci peuvent être classés dans les catégories suivantes :
- Confidentialité : les données synthétisées permettent de reproduire certaines caractéristiques de données existantes mais dont la confidentialité ne permet pas une diffusion ou une utilisation directe. Dans ce cas, ces données, sous réserve de certaines garanties, pourraient apporter le niveau de confidentialité nécessaires à certains cas d’usages, notamment en santé et dans le domaine bancaire.
- Exhaustivité : malgré l’explosion du volume de données collectées dans notre quotidien, les données réelles ne peuvent pas toujours répondre aux besoins de certaines industries pour lesquelles la collecte serait trop coûteuse, ou impossible en vue de l’exhaustivité nécessaire. Ce cas, connu dans le milieu de l’apprentissage machine comme « augmentation des données », est rencontré par exemple dans la simulation de situations de trafic particulières pour l’amélioration des systèmes de navigation des voitures autonomes.
- Spécificité : la rareté de certains évènements, ou leur faible importance relative (problème du déséquilibre des classes) peut rendre leur anticipation difficile, alors que la modularité des données synthétiques permet de générer toutes sortes de situation. Il est possible de générer un évènement difficile à enregistrer en pratique, ou relativement rare, comme une fraude fiscale ou une maladie rare, ou encore un évènement inexistant, c’est le cas des hypertrucages ou deepfakes en anglais.
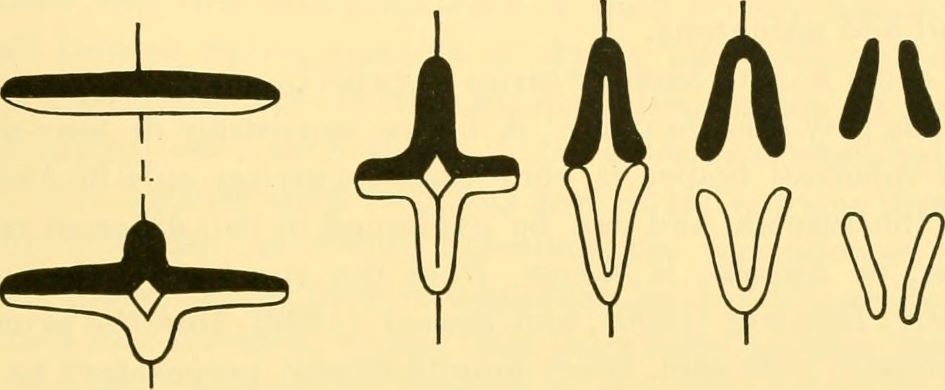
- Exactitude : la fiabilité de certains procédés de synthèse permet de constituer des ensembles de données dénuées des incertitudes portant sur les données réelles. Cette qualité est cruciale dans certains domaines comme l’entraînement des systèmes de vision par ordinateur, où l’annotation généralement réalisée par les humains comporte de nombreuses imprécisions, alors que les données synthétiques seront annotées correctement au pixel près. Un exemple de visage de synthèse et son annotation sont présentés dans la Figure 1, ce type de données peut alors être utilisé pour entraîner un algorithme de segmentation [2].

Figure 1 : Un visage de synthèse et une visualisation de l'annotation qui lui correspond (rouge : nez, verts : yeux, orange : sourcils, etc.) (source)
Ces qualités – bien qu’encore supposées à ce stade pour certaines d’entre elles – justifient l’intérêt porté par les acteurs privés dans ce domaine, tout en s’appuyant de nombreuses avancées provenant du milieu académique.
Un nouveau filon pour le marché de la donnée
Les perspectives ouvertes par le développement des techniques de synthèse, et par le cadre juridique portant sur les traitements de données personnelles offre un environnement propice à l’essor du marché des données synthétiques. Les principaux cas d’usage sont les suivants :
- Entraînement de modèles d’IA : de nombreuses entreprises proposent l’utilisation de données synthétiques pour entraîner des algorithmes comme solution aux besoins spécifiques de cette tâche [3] : un grand volume de données, dont l’annotation est aussi exacte que possible, et sous certaines contraintes de confidentialité.
- Test de logiciels : lorsque les données ne sont pas disponibles à cause de leur rareté, de leur confidentialité ou d’obstacles rendant leur collecte difficile en pratique, certains logiciels peuvent être évalués sur des données synthétiques. C’est le cas pour le test des systèmes opérant sur des transactions financières dont la confidentialité ne permet pas leur réutilisation, du test des voitures autonomes en conditions exhaustives ou encore pour la génération de modèles d’intrusion pour la cybersécurité.
- Partage de données : la confidentialité des données constitue parfois un blocage important pour le partage de données dont l’utilité n’est pas toujours connue a priori mais dont l’ouverture notamment au milieu académique est sollicitée. Certaines données publiées par le Census Bureau américain sont synthétiques, Newsenselab publie également les données concernant les migraines des utilisateurs de son application sous forme synthétique afin d’encourager la recherche académique.
- Génération de contenus de synthèse : ce type de contenu totalement ou partiellement synthétique peut être utilisé de manière loyale pour simuler une situation, comme un essayage vestimentaire, ou à des fins artistiques mais également pour des finalités insidieuses comme la transformation de photos de personnes en images pornographiques.
Si l’adoption des données synthétiques pour chacune de ces tâches suscite encore des doutes de la part de certains ré-utilisateurs, le développement des techniques pourrait permettre une adoption rapide et massive. Les données synthétiques pourraient ainsi représenter 60% des données utilisées pour l’entraînement des systèmes d’IA comme le prédit le cabinet Gartner.
Un procédé statistique pour des données synthétiques
Des données au tout, du tout aux données
En dépit de la grande diversité des techniques de synthèse de données, le concept sur lequel ces dernières reposent est bien unique. La synthèse de données consiste en la reproduction d’une distribution statistique [4], que celle-ci ait été induite à partir d’un ensemble de données source ou qu’elle corresponde à un modèle théorique, dans un ensemble de données généré de manière automatique. En d’autres termes, la synthèse de données consiste en la reproduction d’un système connu théoriquement ou empiriquement dans un ensemble de données où certaines spécificités du système peuvent être volontairement omises et dont on maîtrise les paramètres. Les méthodes permettant d’induire les caractéristiques statistiques, celles permettant de générer les données synthétiques, et l’agencement entre ces deux étapes varient dans les techniques rencontrées et permettent de classer ces dernières.
Modélisation théorique puis génération
Tout d’abord, certaines méthodes modélisent la distribution des données sources selon une loi de probabilité théorique ou hypothétique. Cela peut être le cas lorsqu’on connaît les lois (mécaniques, biologiques, ou encore économiques) régissant le système étudié ou lorsqu’une loi semble naturelle pour représenter le phénomène [5]. La loi obtenue est alors paramétrée pour coller aux données et représenter au mieux le système. Enfin, une méthode comme la méthode de Monte-Carlo est utilisée pour générer des données en suivant la loi de probabilité obtenue.
Si cette méthode est la plus simple à mettre en place, c’est également celle qui réalise les hypothèses les plus fortes sur les données source, de telle sorte que la représentation obtenue est généralement trop simpliste. Elle est toutefois utilisée pour générer des simulations comme dans les tests de voitures autonomes. Dans ce domaine, la dynamique de chacun des éléments du système est bien connue, mais leur association, à laquelle s’ajoutent des phénomènes aléatoires, nécessite une simulation pour en connaître le comportement.
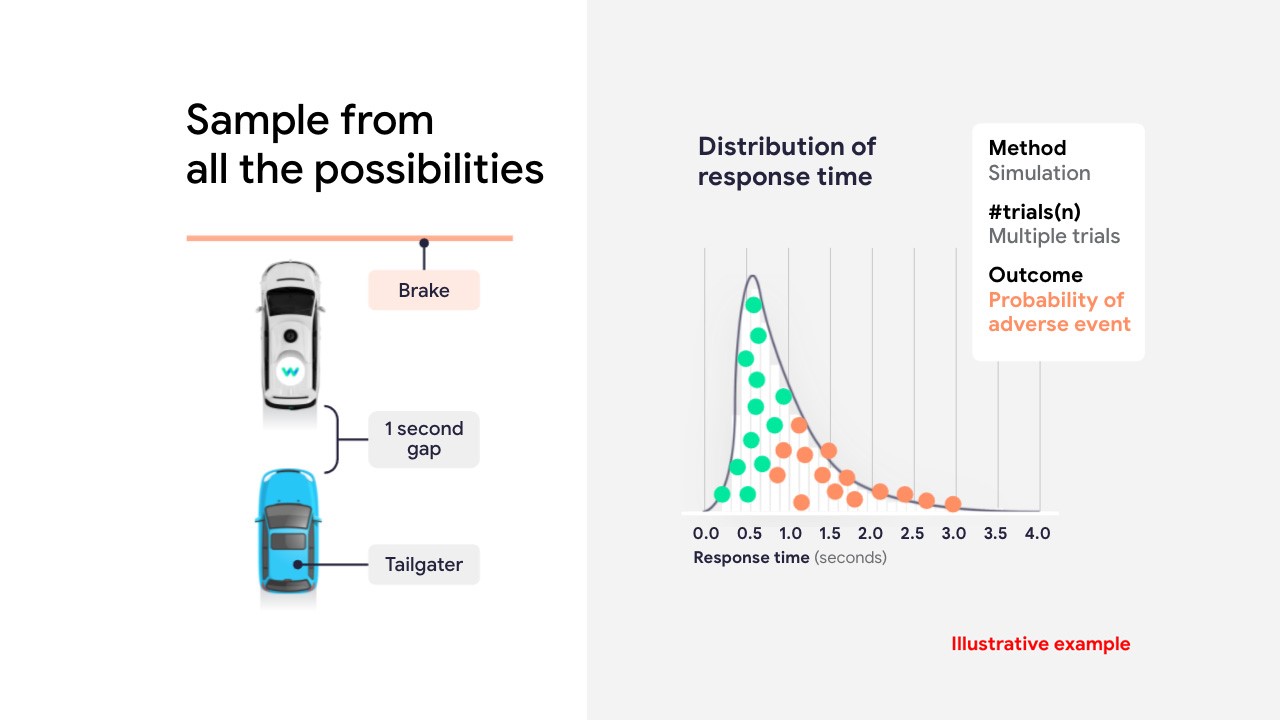
Figure 2 : simulations de scenarios de freinage selon une loi de probabilité connue (source)
Dans la Figure 2, le système considéré est une voiture autonome dont on cherche à simuler le freinage. Le temps nécessaire à celui-ci dépend des conditions météorologiques, de l’usure des pneus, de la visibilité et de multiples autres facteurs qui agissent sur le système de telle sorte que le temps de freinage suit une distribution décrite par la distribution visualisée sur la courbe de droite (obtenue grâce à une série de tests en conditions réelles par exemple). Grâce à la connaissance de cette distribution, il est possible de simuler les cas extrêmes (temps de réponse de plus de deux secondes par exemple), d’en connaître les conséquences et la probabilité de leur occurrence.
Modélisation heuristique explicite puis génération
La seconde catégorie de méthodes utilisées pour générer des données synthétiques est similaire à la précédente dans son déroulé, seule la modélisation de la distribution des données diffère : elle est ici réalisée de manière heuristique, c’est-à-dire que le modèle est induit empiriquement à partir des données. Afin de déterminer les lois de probabilités décrivant les données sources, un modèle est choisi (réseau bayésien, arbres de décision, copules, etc.) et entraîné pour représenter au mieux les données. En pratique, un arbre de décision par exemple, pourra se voir imposer sa structure (nombre d’embranchements et profondeur des branches) avant que les logiques représentées par ces embranchements ne soient trouvées et paramétrées. Enfin, une méthode classique de génération de données est utilisée pour synthétiser les données depuis le modèle.
Ces méthodes permettent de représenter des phénomènes plus complexes que la méthode précédente, toutefois elles ne parviennent pas à représenter tous les phénomènes. Leur avantage est d’être facilement interprétable. Cette méthode, utilisant les réseaux bayésiens, a été utilisée par le Census Bureau américain afin de publier des données synthétiques générées à partir des données de recensement.
En ce que le modèle est paramétré pour coller au mieux aux données, cette méthode est heuristique et diffère de l’approche théorique précédente. La représentation des données, elle, reste explicite puisque les distributions peuvent être retrouvées dans le modèle obtenu.
Modélisation heuristique explicite et génération
Une approche utilisant des réseaux de neurones pour représenter la distribution des données sources a été proposée par (Kingma et Welling, 2013). En partant d’une méthode existante, les auto-encodeurs, les auteurs de cette publication définissent les auto-encodeurs variationnels, ou variationnal autoencoders (VAE), dont l’un des atouts est d’améliorer leur capacité à générer des données. Cette méthode permet d’approximer la distribution des données sources dans un « espace latent » formel et explicite [6] grâce à un réseau de neurones, puis de générer des données de synthèse grâce à un second réseau. L’entraînement des deux réseaux a ainsi lieu simultanément, et leur objectif commun est de générer un ensemble de données de synthèse suffisamment proche des données sources.
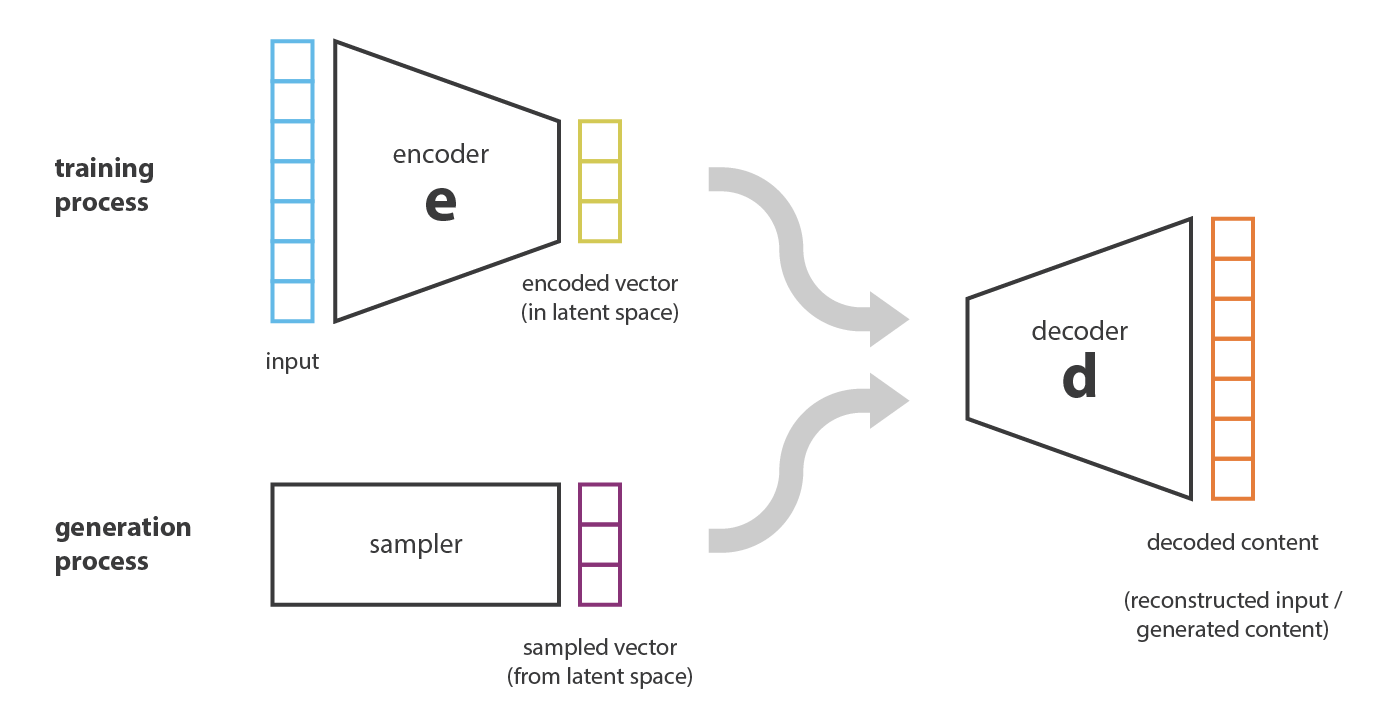
La Figure 3 distingue la phase d’entraînement d’un VAE de celle de génération. Lors de l’entraînement la donnée d’entrée ou input, c’est-à-dire l’ensemble source, est encodée par l’encodeur sous une représentation vectorielle (représentation statistique des données), avant d’être décodée en un ensemble de synthèse par le décodeur. Les ensembles source et de synthèse sont comparés et les paramètres de l’encodeur et du décodeur sont adaptés pour faire en sorte de rapprocher statistiquement ces deux ensembles. En ce qui concerne la synthèse, la représentation vectorielle est utilisée pour générer directement des données, généralement grâce à des procédés aléatoires.
Les VAE possèdent l’avantage de permettre une génération de données en grande quantité avec un besoin computationnel moins important que les méthodes citées précédemment. Toutefois, il apparaît que leur utilisation se généralise mal à des données dont les caractéristiques ne sont pas toutes de même nature (lorsque certaines sont des variables catégorielles et d’autres des variables continues par exemple).
Modélisation heuristique implicite et génération
Enfin, une approche novatrice proposée par (Goodfellow et al., 2014) réunit les étapes de génération des données de synthèse et la modélisation de leur distribution. Alors que les deux étapes étaient jusqu’alors successives, ici, les deux algorithmes sont entraînés de manière simultanée et sont en compétition. En pratique, il s’agit d’un algorithme génératif, en charge de générer des données de synthèse, et d’un algorithme discriminant, dont la tâche est de distinguer les contenus de synthèse des contenus réels. Plusieurs types d’algorithmes peuvent être utilisés pour ces tâches bien que des réseaux de neurones soient le plus souvent utilisés, on parle alors de réseaux antagonistes génératifs, ou generative adversarial networks (GAN).
Avec cette approche qui ne modélise pas explicitement la distribution des données, il est généralement plus difficile d’interpréter les résultats obtenus. En particulier, les caractéristiques de l’ensemble d’entraînement qui auront effectivement été apprises par le réseau – et donc reproduites dans les données de synthèse – ne sont pas toujours facilement identifiables.
Les GAN, qui existent dans une grande diversité d’implémentations, sont les algorithmes généralement cités par les entreprises commercialisant des données de synthèse. Ainsi, leur utilisation est retrouvée dans plusieurs domaines allant de la recherche médicale à la détection de fraudes bancaires, en passant par la génération d’hypertrucages (« deepfakes »).
L’apprentissage de Turing : les réseaux antagonistes
L’apprentissage de Turing désigne une méthode particulière permettant d’entraîner un algorithme à réaliser une tâche en mettant en jeu une étape similaire au test de Turing. Ce test décrit en 1950 par le mathématicien et cryptologue anglais Alan Turing vise à confronter un agent humain à une machine qui doit se faire passer pour un autre humain, le test étant réussi lorsque la machine parvient à tromper l’agent et à se faire passer pour un humain. Ici on confronte deux algorithmes, le premier, appelé génératif, effectue une tâche de synthèse (de données tabulaires, d’images, de vidéos, etc.) alors que le second, appelé discriminant, doit déterminer si les données qui lui sont fournies sont authentiques ou de synthèse. Dans cette compétition, les deux algorithmes parviennent à améliorer réciproquement leurs performances et cette procédure permet ainsi d’obtenir un réseau génératif et un réseau discriminant pouvant être utilisés dans des contextes différents.
Cette approche a été proposée par Ian Goodfellow pour la première fois dans son article introduisant les GAN. Alors que l’apprentissage de Turing pourrait s’appliquer à tous les types d’algorithmes, ce sont ici des réseaux de neurones qui sont utilisés. En pratique, le réseau discriminant est entraîné sur un ensemble de données de départ jusqu’à ce qu’il atteigne une performance suffisante. Le réseau génératif est alors alimenté par du bruit blanc [7] et produit des visages qui sont fournis au réseau discriminant. Ce dernier indique s’il juge que l’image est authentique ou non, et ce résultat est comparé à la réalité. Le résultat est une indication de la performance des deux réseaux et permet de les améliorer respectivement dans une dernière phase appelée rétropropagation.
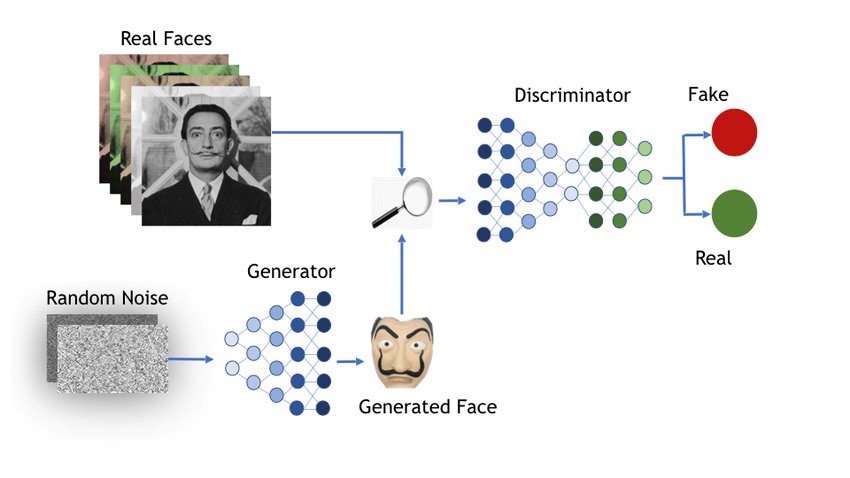
Figure 4 : Entraînement des GAN pour la synthèse de visage (source)
Après un certain nombre d’itérations, les deux réseaux atteignent généralement un statu quo où chacun parvient à tromper l’autre en moyenne une fois sur deux : ce résultat est garanti par la théorie des jeux car il s’agit d’un jeu à somme nulle [8]. Toutefois, cette situation ne garantit pas la qualité des prédictions des deux réseaux, un réseaux génératif imparfait pouvant parfois tromper un réseau discriminant lui aussi imparfait. Ce phénomène, qui correspond en quelques sortes à un équilibre sous-optimal (ou minimum local en termes d’optimisation), est caractérisé par des données de synthèse imparfaites et répétitives, et est connu sous le nom d’effondrement des modes. Ce problème est l’une des trois difficultés principales rencontrées dans l’apprentissage de Turing, avec la disparition du gradient et l’instabilité de la convergence également rencontrées dans d’autres domaines de l’apprentissage automatique.
Il existe une très grande variété d’implémentation des méthodes décrites précédemment visant généralement à générer un gain en termes de besoins computationnels, de représentation des données sources, ou encore de protection de la vie privée. Ainsi, on trouve dans la littérature des algorithmes hybrides, tels que les Copula-GAN ou les VAE-GAN. Mais également des implémentations utilisant d’autres techniques telles que la confidentialité différentielle ou differential privacy : (Bindschaedler et al., 2017) utilise ce concept pour réduire le risque de réidentification lié à un ensemble de données de synthèse généré grâce à une méthode statistique (appartenant ainsi à la seconde des classes définies plus haut). Cette méthode est supposée donner une garantie formelle concernant le risque de réidentification portant sur les données, bien que son implémentation soit complexe en pratique.
Voir l'article suivant : « [Données synthétiques] - Et l'Homme créa les données à son image »
Notes
[1] Comme en témoignent les mouvement financiers dans le domaine : achat de Twenty Billion Neurons par Qualcomm en juillet 2021, acquisition de AI.Reverie par Facebook en octobre 2021, levée de fonds par Hazy en 2020, etc.
[2] La segmentation d’image consiste à identifier et regrouper entre eux les pixels appartenants à un même objet où à la même partie d’un objet (cheveux, nez, voiture, piéton, etc.).
[3] Cet article de AIMultiple donne un tour d’horizon de ces entreprises (dont MostlyAI, Hazy, Statice, etc.)
[4] Une distribution est la répartition d’un échantillon de données selon une loi de probabilité comme une loi uniforme, ou une gaussienne. Un ensemble de données comportant plusieurs variables est généralement caractérisé par plusieurs distributions et des corrélations entre les variables.
[5] La loi gaussienne par exemple est fréquemment utilisée pour représenter des phénomènes résultants de multiples facteurs supposés indépendants, comme la répartition de la taille ou du poids dans la population.
[6] En pratique, on fait l’hypothèse que les données suivent une distribution gaussienne. Ce sont ainsi la moyenne et l’écart type des lois gaussiennes qui sont approximées lors de l’entraînement.
[7] Cette technique est souvent utilisée en apprentissage automatique afin de donner un point initial à l’algorithme indépendant de toute hypothèse, ce qui évite de biaiser l’algorithme ou de l’induire dans une direction qui ne serait pas la direction optimale.
[8] La fonction de coût d’un réseau augmente quand celle de son adversaire diminue, et puisque chacun cherche à minimiser sa propre fonction, l’entraînement converge lorsqu’un équilibre (appelé équilibre de Nash) est atteint. Ce schéma correspond à celui d’un jeu à somme nulle en théorie des jeux.


