[2/3] Advanced privacy-preserving cryptographic techniques

Summary

 

• Introductory article: Experts provide the keys to deciphering today’s and tomorrow’s cryptography
• Article 1: Post-quantum cryptography
• Article 2: Advanced privacy-preserving cryptographic techniques
• Article 3: Practical applications of advanced cryptography

 

Operations on encrypted data

 

Encryption is the main technique used to ensure data confidentiality. However, the need to process this data while preserving its confidentiality poses a major challenge. All the experts interviewed discussed the emerging opportunities and challenges associated with operations on encrypted data.

 

 

Fully homomorphic encryption (FHE)

 

Homomorphic encryption allows mathematical operations to be performed on encrypted data without knowing the underlying plaintext data. In practical terms, this means that calculations can be performed directly on the encrypted data, producing an encrypted result which, once decrypted, corresponds to the result of the calculation as if it had been performed on the plaintext data.

 

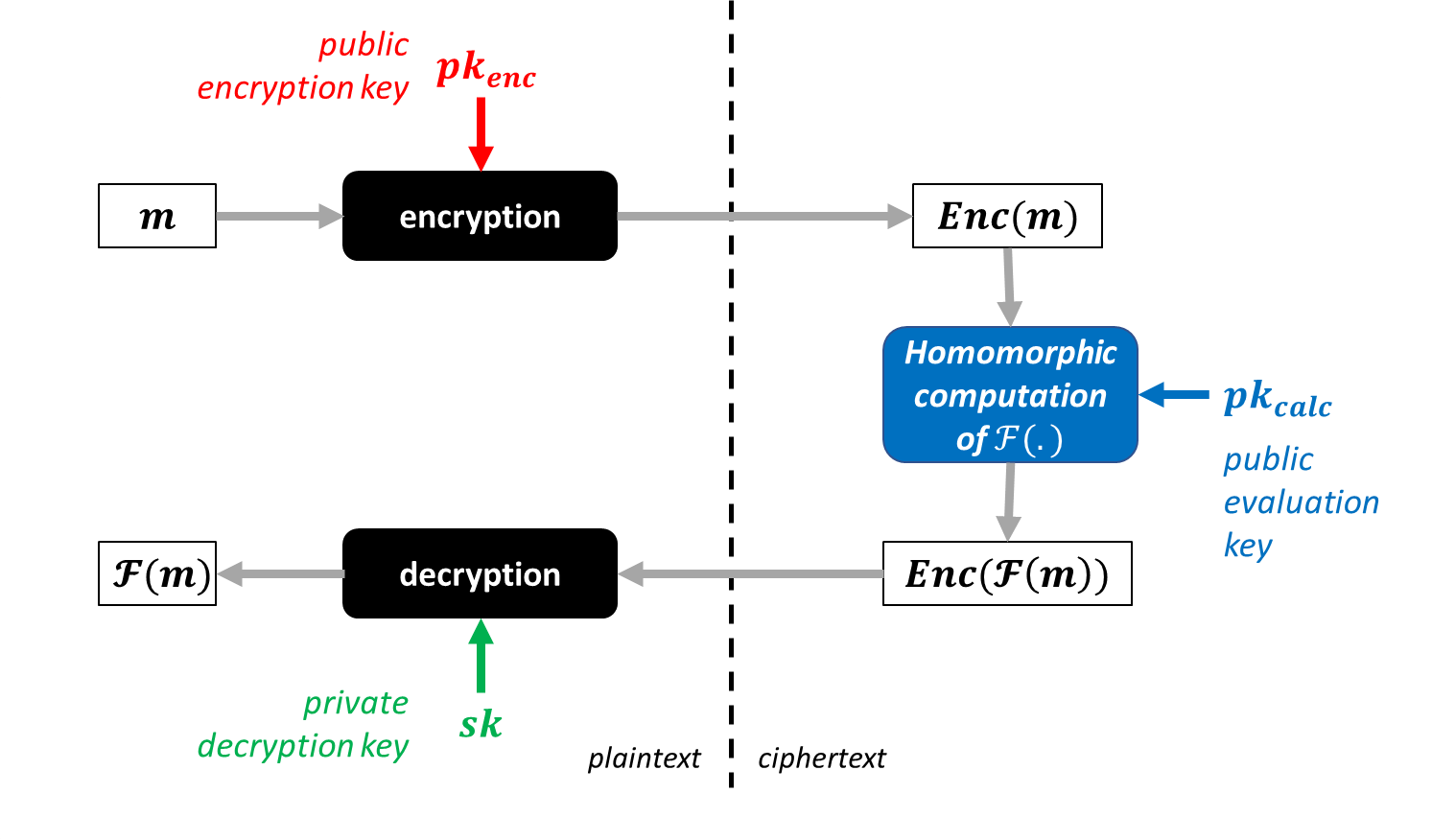
Descriptive diagram of homomorphic encryption

 

More specifically, there are several classes of homomorphic encryption, depending on the complexity of the operations that can be performed on the ciphertext: 

•  « Partially homomorphic » encryption only allows one type of operation to be performed: addition or multiplication. Although less general in use than somewhat homomorphic or fully homomorphic encryption (see below), it is of great interest due to its greater efficiency. Classic examples include private information retrieval (PIR), which is similar to an online search without revealing the search terms to the search engine, which can be performed with partially homomorphic encryption.

• Somewhat homomorphic encryption allows a small number of operations to be performed before the resulting ciphertext becomes impossible to decrypt.

• Fully homomorphic encryption (FHE) allows arbitrary operations to be performed on ciphertexts and therefore has the most applications in theory.

 

First imagined in the late 1970s, a first theoretical realisation of Fully Homomorphic Encryption (FHE) only appeared in 2009 thanks to the work of Craig Gentry [1]. The mechanism proposed by Gentry relied on lattices but was not efficient in practice. Its use was limited by excessive complexity and significant performance costs compared to computations on plaintext data. Since then, fuelled by renewed industrial interest, FHE has made significant progress in terms of practicality, thanks to continuous advances in algorithms, hardware performance, and software optimization.

 

The opportunities for homomorphic encryption

One of the experts provided an overview of the solutions proposed by stakeholders in this ecosystem:

 

• At the hardware level: computations using FHE on encrypted data require far more operations than computations on unencrypted data. To enable faster processing, hardware acceleration may be necessary. Companies such as Intel, Optalysys, and Galois Inc. are developing processors specifically designed to perform the required resource-intensive mathematical operations.

 

• At the software level: the availability of software libraries, i.e., computer code providing specific functionalities for FHE and intended for developers, is a major asset for the democratisation of homomorphic encryption. Industry leaders such as IBM and Microsoft respectively offer the HELib and SEAL libraries. Other smaller companies are also active in this field (Duality Technologies, Inpher, Cosmian, etc.).

 

• At the compiler level: FHE compilers are software tools that simplify the programming of functions that can be executed in the encrypted domain. They enable to translate computer programs into FHE-compatible instructions, thereby facilitating the adaptation of existing programs. Google and the French startup Zama both offer such compilers. The CEA also provides its own compiler, Cingulata from CEA-LIST, as an open-source project.

 

Most of the interviewed experts acknowledged that the FHE tools available today already enable to start using the technology, even for non-cryptography experts. In terms of efficiency, FHE is steadily progressing toward greater practicality, but it still requires significant technological investments before it can be broadly deployed in industry. 

 

Other research perspectives around FHE were also discussed during the interviews:

 

• The first research avenue concerns scenarios involving multiple data sources that wish to perform computations on their pooled data. Standard FHE does not support this type of configuration, and in such cases, multi-party FHE or multi-key FHE should be prioritised.

 

• The second research avenue focuses on verifying the correctness and integrity of computations performed under FHE (« verifiable FHE »). This applies to the case of a cloud server executing computations delegated by a client, where the accuracy of the computation on encrypted data could be compromised. Verifiable FHE solutions would allow the client to verify the integrity of the computations carried out on the encrypted data, based on a proof generated by the cloud. The key challenge lies in ensuring that verifying the proof is more efficient than having the client perform the computation themselves.

 

Functional Encryption

 

Some experts mentioned functional encryption as a complementary tool for performing operations on encrypted data. It consists of encrypting data in such a way that it can be selectively decrypted, depending on the operations the user is authorised to perform. Functional encryption thus makes it possible to control access to data according to the specific functions each user is allowed to execute. For each function, a specific decryption key is generated. 

In FHE, any computation is theoretically possible on the encrypted data, but the result remains encrypted and must be sent back to the holder of the decryption key in order to access it in cleartext. With functional encryption, however, the result of the computation is directly accessible in cleartext after the operation, but the data holder can only perform computations explicitly authorised by the data owner. Depending on the specific use cases, one or the other of these techniques may therefore prove more suitable.

 

 

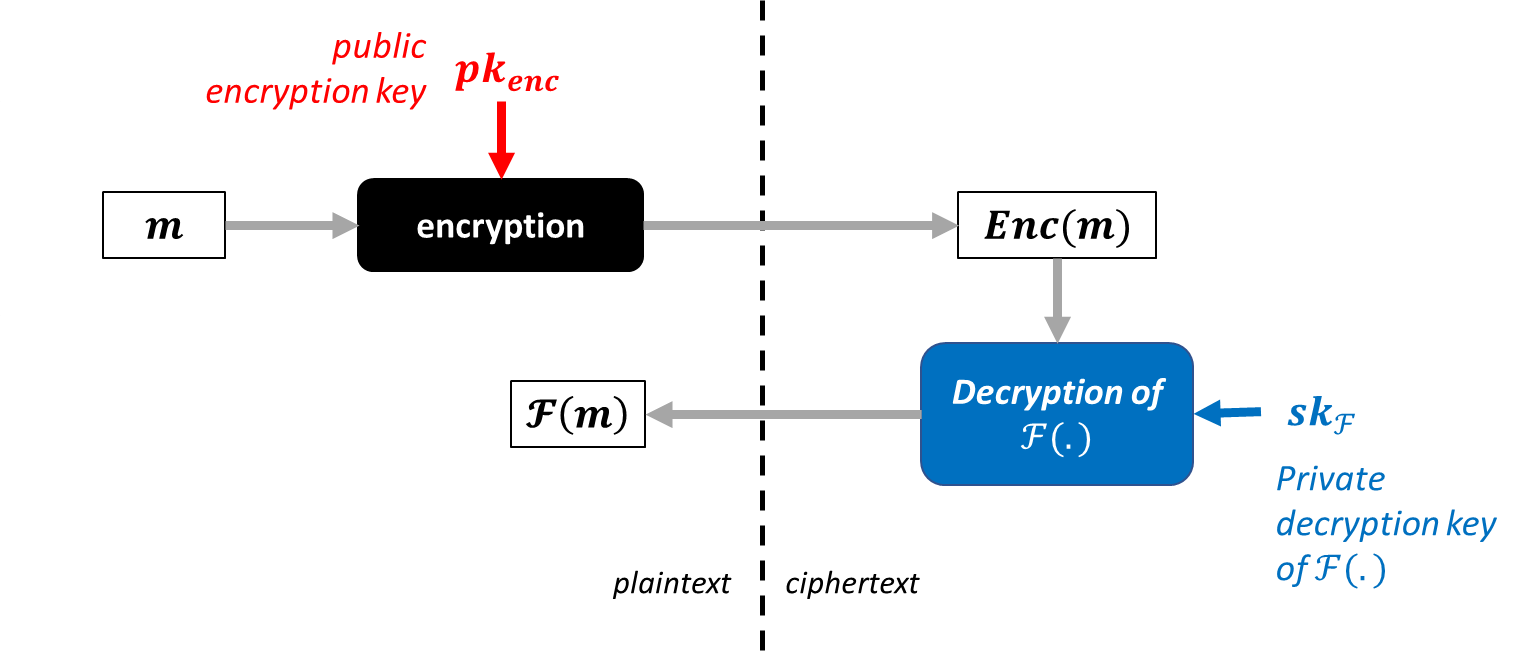
Descriptive diagram of functional encryption

 

Today, functional encryption is still in its early stages. In terms of efficiency, research in this field has primarily focused on specific operations, such as the inner product, for which solutions have been developed to improve performance and practicality. However, when it comes to applying functional encryption to more general and complex functions, performance remains prohibitive for large-scale deployment.

It is therefore an active area of research, aimed at making functional encryption more efficient and practical.

 

Secure Multiparty Computation (MPC)

 

To perform computations on encrypted data, MPC was also discussed during interviews with experts. This branch of cryptography, which emerged in the 1980s, has been extensively explored since then. MPC has continuously evolved over the years, becoming increasingly practical and applicable to various use cases.

One of the first MPC protocols, the « garbled circuit », was proposed by Andrew Yao in 1982. In his study, Yao introduced the famous « millionaires’ problem »: two millionaires want to determine which of them is richer, without revealing the exact value of their wealth to each other. A naïve but complex solution would involve a trusted third party: each millionaire would communicate the value of their wealth to this third party, who could then determine who is richer without revealing any other information. MPC techniques aim to replicate this scenario without relying on a trusted third party, while ensuring the same guarantees of confidentiality and correctness of the result.

In an MPC protocol, a set of parties, who do not trust each other, collaborate to jointly compute a function over their data without ever revealing anything about their initial inputs to the other participants, except what is implied by the final result of the function. This process relies on advanced cryptographic techniques (secure secret sharing, oblivious transfer, homomorphic encryption, etc.) and on communication among the participants.

 

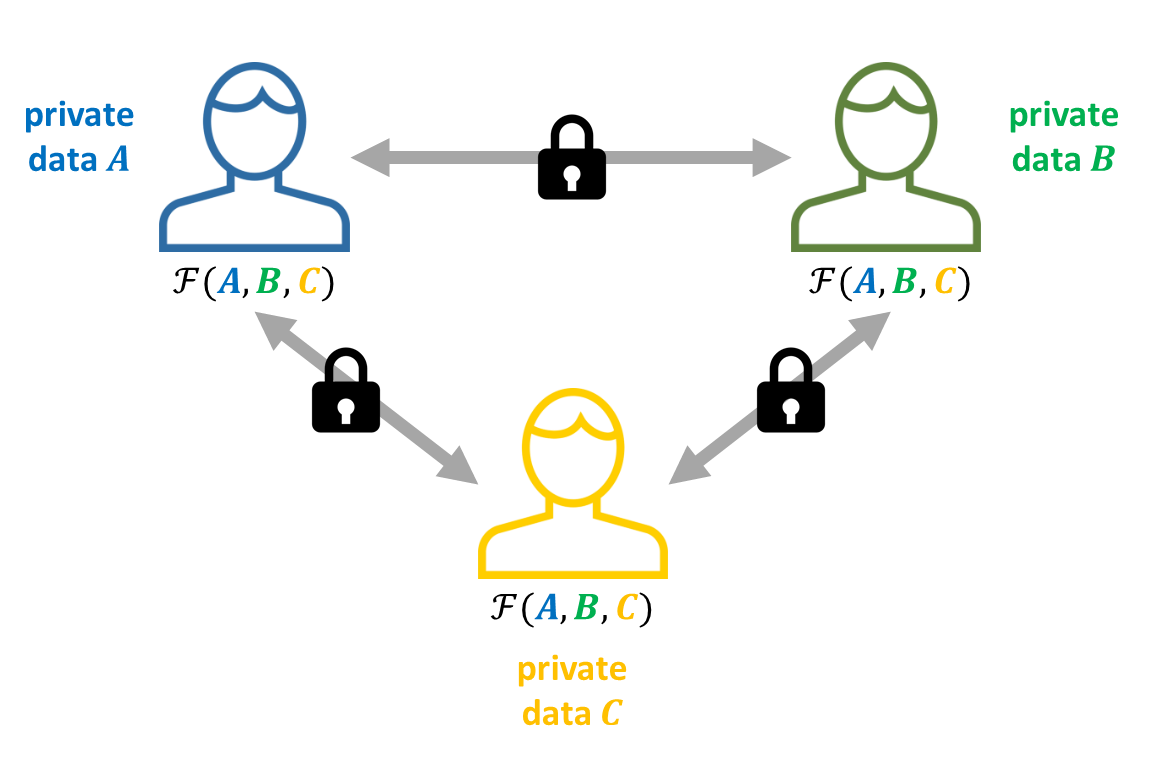
Descriptive diagram of secure multiparty computation of a function F

 

There are two main types of MPC protocols:

 

• Generic protocols, which allow the computation of an arbitrary function on the parties’ data. They can be flexible and suitable for various applications, but may be complex and costly to implement;

 

• Specialised, or ad-hoc protocols, which are designed for specific functions chosen in advance. These protocols are optimised for these particular tasks and are often more efficient in terms of computation time and required resources. They have been studied enough to be usable today. This is particularly the case for protocols enabling the computation of private set intersections (see below), whose computation times have been significantly reduced compared to the early versions of these protocols.

 

Some of the experts mentioned tools for developing MPC-based solutions (namely SCALE-MAMBA and MP-SPDZ). These open-source tools can be used to compile a general function into a secure MPC protocol.

In recent years, advances in MPC have made it possible to consider implementing systems based on this paradigm. In addition, MPC-based applications are often more mature than applications based solely on homomorphic encryption. This is because homomorphic encryption remains more expensive than MPC, particularly for large-scale operations. For several years now, there have been concrete applications of MPC:

 

• In Denmark, in 2008, an auction of sugar beets was secured using MPC;
• In Boston, since 2016, studies on gender pay inequality commissioned by the Boston Women's Workforce Council have been conducted using MPC techniques. 

 

 

Zero-knowledge proofs

 

Some of the experts interviewed identified zero-knowledge proofs (ZKPs) as cryptographic mechanisms that could be immediately deployed in various real-world use cases. Proofs of concept already exist, particularly in the context of privacy-friendly age verification. ZKPs are also promoted by a number of experts for the implementation of future European digital identity wallets planned under the European Union Regulation on electronic identification and trust services for electronic transactions in the internal market (eIDAS 2 Regulation). 

These proofs, introduced in the 1980s, make it possible to prove that a condition (or assertion) is true without revealing the underlying information, thereby ensuring confidentiality. They can be useful in many scenarios: proving that a data subject is of legal age without revealing their identity, proving that they have a certain amount of money without revealing their bank account balance, etc.

ZKPs still present significant challenges in terms of implementation. Their design requires expertise in advanced cryptography, and translating them into real-world applications requires a thorough understanding of the underlying concepts.

Furthermore, the practical implementation of ZKPs can sometimes require significant computing power. For applications such as age verification, where a server does not need to verify a large number of proofs simultaneously, this may not pose a major problem. However, for large-scale applications, such as the use of ZKPs in blockchain, response times can be crucial. Finding the best compromise between privacy and performance remains a major challenge: some protocols may sacrifice a little privacy for better performance, or vice versa. 

Moreover, another challenge lies in the fact that some ZKP systems require a trusted setup phase to generate the initial parameters necessary for the execution of the proof protocol. This phase may involve trust assumptions that are too demanding in real-world scenarios.

 

However, ZKPs are still evolving and gaining maturity. Research in this field is focusing in particular on improving computational efficiency, reducing resource requirements, and standardisation for widespread adoption. These advances may even be accelerated by the explicit mention of ZKPs in recital 14 of the eIDAS 2 regulation.

In the near future, the experts anticipate a more widespread integration of ZKPs as these systems become more efficient. Moreover, ZKP solutions robust to quantum attacks exist and are currently subjects of ongoing research. Other research directions aim to combine ZKPs with, or construct them from, other cryptographic building blocks. For instance, « MPC-in-the-head », a paradigm for building a ZKP system from a multiparty computation (MPC) protocol, has been the subject of several scientific publications. Other ongoing work combines ZKPs with FHE to ensure confidentiality and verifiability of computations on encrypted data, as discussed earlier. 

 

Group Signatures

 

This technology was introduced in the 1990s by Chaum and van Heyst. It refers to a type of digital signature for a group of people. The group is associated with a single public key used to verify signatures. Each member of the group has their own private signing key, which allows them to generate signatures that can be verified using the group’s public key. This type of signature enables a group member to prove their membership without revealing their individual identity (i.e., in practice, it is difficult to determine which group member generated the signature). Each group member can sign messages on behalf of the group, and, like any digital signature, anyone can verify the signature. It is also possible to give a trusted authority the ability to reveal the identity of the signer.

Group signatures are a well-established cryptographic mechanism. Certain forms of group signatures are already standardised by the ISO (International Organization for Standardization) under the ISO/IEC 20008 standard. Group signatures are used in industry, particularly in TPM (Trusted Platform Module) cryptoprocessors, in the form of Direct Anonymous Attestations, a cryptographic primitive that allows remote authentication of the TPM while preserving the identity of the user of the platform containing the module. A similar approach is employed in Intel processors through EPID (Enhanced Privacy ID).

 

Nevertheless, one of the experts expressed regret that group signatures remain largely confined to research and development, despite the existence of efficient implementations and established standards. One practical application mentioned, which could work effectively in practice, is the use of group signatures to control access to a building entrance or to perform privacy-preserving age verification. In this regard, LINC has published a demonstrator of an age verification mechanism based on group signatures. 

 

Conclusion

 

At a time when privacy protection is a major concern, interviews with cryptography experts have provided several key insights.

The emergence of privacy-enhancing technologies (PETs) such as homomorphic encryption (FHE), zero-knowledge proofs (ZKP), and group signatures offers innovative solutions to address these concerns. Despite significant progress in these areas, challenges remain, particularly regarding performance and practicality. However, with growing industry interest and ongoing research efforts, the widespread adoption of these technologies appears increasingly realistic.

Although the GDPR does not explicitly mention these technologies, its Article 25 on « data protection by design and by default » underscores the importance they could have in fulfilling this obligation. The CNIL could promote and encourage their use in implementing the regulation to further strengthen the protection of personal data.

 

 

[1] Gentry, C. (2009, Mai). Fully homomorphic encryption using ideal lattices. In Proceedings of the forty-first annual ACM symposium on Theory of computing (pp. 169-178).

 

 

Illustration : pexels